498. Diagonal Traverse

題目

Given an m x n matrix mat, return an array of all the elements of the array in a diagonal order.

Example 1:

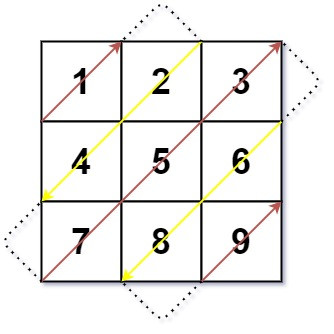
Input: mat = [[1,2,3],[4,5,6],[7,8,9]]
Output: [1,2,4,7,5,3,6,8,9]

Example 2:

Input: mat = [[1,2],[3,4]]
Output: [1,2,3,4]

Constraints:

• m == mat.length
• n == mat[i].length
• 1 <= m, n <= 104
• 1 <= m * n <= 104
• 105 <= mat[i][j] <= 105

解法(Java)

這題解法是由幾個if-else 判斷組成的，要判斷什麼時候往右上走或是往左下走，到後半部分轉換的時候也要注意邊界問題，所以判斷的先後順序也要調整。

首先，座標和為0或偶數時往右上走，反之則往左下走，再來自己畫33 跟44 的圖，比較一下邊界應該就知道座標怎麼加減了。

Runtime: 2 ms (98.5%)
Memory Usage: 46.2 MB (42.51%)

class Solution {
    public int[] findDiagonalOrder(int[][] mat) {
        int m = 0, n = 0;
        int[] result = new int[mat.length * mat[0].length];

        for (int i = 0, size = result.length, ml = mat.length - 1, nl = mat[0].length  -1; i < size; i++) {
            result[i] = mat[m][n];

            if ((m + n) % 2 == 0) {
                if (n == nl) m++;
                else if (m == 0) n++;
                else {
                    m--;
                    n++;
                }
            } else {
                if (m == ml) n++;
                else if (n == 0) m++;
                else {
                    m++;
                    n--;
                }
            }
        }

        return result;
    }
}

54. Spiral Matrix

題目

Given an m x n matrix, return all elements of the matrix in spiral order.

Example 1:

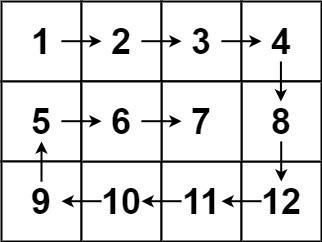
Input: matrix = [[1,2,3],[4,5,6],[7,8,9]]
Output: [1,2,3,6,9,8,7,4,5]

Example 2:

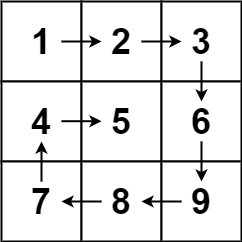
Input: matrix = [[1,2,3,4],[5,6,7,8],[9,10,11,12]]
Output: [1,2,3,4,8,12,11,10,9,5,6,7]

Constraints:

• m == matrix.length
• n == matrix[i].length
• 1 <= m, n <= 10
• 100 <= matrix[i][j] <= 100

解法(Java)

第一個解法是優化前的做法，使用多個變數儲存m 和n 的最大及最小值，當遇到邊界時則轉向。

Runtime: 0 ms (100%)
Memory Usage: 40.9 MB (18.93%)

class Solution {
    public List<Integer> spiralOrder(int[][] matrix) {
        List<Integer> result = new ArrayList<>();
        int mMin = 0, mMax = matrix.length - 1, nMin = 0, nMax = matrix[0].length - 1;

        int m = 0, n = 0, direct = 0;
        for (int i = 0; i < matrix.length*matrix[0].length; i++) {
            result.add(matrix[m][n]);

            switch (direct) {
                case 0:
                    if (n != nMax) {
                        n++;
                    } else {
                        m++;
                        mMin++;
                        direct = 1;
                    }
                    break;
                case 1:
                    if (m != mMax) {
                        m++;
                    } else {
                        n--;
                        nMax--;
                        direct = 2;
                    }
                    break;
                case 2:
                    if (n != nMin) {
                        n--;
                    } else {
                        m--;
                        mMax--;
                        direct = 3;
                    }
                    break;
                case 3:
                    if (m != mMin) {
                        m--;
                    } else {
                        n++;
                        nMin++;
                        direct = 0;
                    }
                    break;
            }
        }

        return result;
    }
}

由於第一個解法在記憶體表現上不佳，繼續思考解法後發現並不需要特別使用m 和n 去移動座標，只會在某一個邊界上移動，因此可以省去一些變數。

Runtime: 0 ms (100%)
Memory Usage: 40.2 MB (87.39%)

class Solution {
    public List<Integer> spiralOrder(int[][] matrix) {
        List<Integer> result = new ArrayList<>();
        int mMin = 0, mMax = matrix.length - 1, nMin = 0, nMax = matrix[0].length - 1;

        while (mMin <= mMax && nMin <= nMax) {
            // right
            if (mMin <= mMax && nMin <= nMax) {
                for (int i = nMin; i <= nMax; i++) {
                    result.add(matrix[mMin][i]);
                }
                mMin++;
            }

            // down
            if (mMin <= mMax && nMin <= nMax) {
                for (int i = mMin; i <= mMax; i++) {
                    result.add(matrix[i][nMax]);
                }
                nMax--;
            }

            // left
            if (mMin <= mMax && nMin <= nMax) {
                for (int i = nMax; i >= nMin; i--) {
                    result.add(matrix[mMax][i]);
                }
                mMax--;
            }

            // up
            if (mMin <= mMax && nMin <= nMax) {
                for (int i = mMax; i >= mMin; i--) {
                    result.add(matrix[i][nMin]);
                }
                nMin++;
            }
        }

        return result;
    }
}

小結

這兩題都是Medium 的題目，解法上需要再多考慮各種情況，常常寫出一個解法但在某些情況下會出錯，在加了一堆判斷想要規避例外狀況後，發現應該是解法上的問題，因此解題上應該要習慣拿紙筆出來，做一些筆記跟計算才比較容易想出解法。